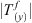| Issue |
EPJ Applied Metamaterials
Volume 2, 2015
Advanced Metamaterials in Microwaves, Optics and Mechanics
|
|
|---|---|---|
| Article Number | 15 | |
| Number of page(s) | 12 | |
| DOI | https://doi.org/10.1051/epjam/2015019 | |
| Published online | 08 February 2016 | |
https://doi.org/10.1051/epjam/2015019
Review
Controlling THz and far-IR waves with chiral and bianisotropic metamaterials
1
Institute of Electronic Structure and Laser, Foundation for Research & Technology-Hellas, N. Plastira 100, 70013
Heraklion, Crete, Greece
2
Ames Laboratory-USDOE, and Department of Physics and Astronomy, Iowa State University, 50011
Ames, Iowa
3
Department of Materials Science and Technology, University of Crete, 71003
Heraklion, Crete, Greece
* e-mail: kafesaki@iesl.forth.gr
Received:
7
December
2015
Accepted:
7
December
2015
Published online: 8 February 2016
Chiral and bianisotropic metamaterials, where coupling of magnetic and electric phenomena plays an important role, offer advanced possibilities for the control and manipulation of electromagnetic waves. Such a control is particularly useful in the THz and far-IR region where natural materials do not show strong response and thus they are not offered as components for a direct realization of electromagnetic wave manipulation. Among the most useful and important capabilities of chiral and bianisotropic metamaterials is the advanced control of the wave polarization that they offer, including giant polarization rotation, conversion, filtering, absorption, etc. In this paper we review our recent work demonstrating some of those capabilities, in a variety of structures, both planar and 3D-bulk ones. The structures presented show, among others, large optical activity, tunable/switchable wave ellipticity, and polarization-dependent asymmetric transmission.
Key words: Metamaterials / Chiral media / Photoconductive silicon / Split-cube resonators / Asymmetric transmission / Direct laser writing
© G. Kenanakis et al., Published by EDP Sciences, 2016
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Metamaterials are tailored man-made composite structured materials with novel and unique electromagnetic properties, different from those of their constituent components. These properties mainly result from the geometry of their building units – often called meta-atoms. By properly designing these units one can achieve unique electromagnetic (EM) properties, beyond those of natural materials, such as negative magnetic permeability, negative refractive index [1–3], refractive index close to zero [4, 5], hyperbolic dispersion relation [6], etc.; such properties empower metamaterials with unique possibilities for the control of electromagnetic waves [3], enabling new solutions in a variety of potential applications, from telecommunications and information processing, to imaging, security, sensing, etc. [7].
A particularly interesting category of metamaterials is that of chiral metamaterials (i.e. metamaterials without any mirror symmetry plane) where electric (magnetic) field creates not only electric (magnetic) but also magnetic (electric) polarization [8]. Chiral metamaterials offer great possibilities in the control of light polarization, [9–16] e.g. optical activity (i.e. polarization rotation of a linearly polarized wave) and circular dichroism (i.e. different absorption between left- and right-handed circularly polarized waves) which can exceed the corresponding effects in natural chiral materials by orders of magnitude [10, 17, 18]. Furthermore, huge chirality in chiral metamaterials was also recently proposed to reduce the attractive Casimir force which is detrimental in micro- and nano-electromechanical systems [19–21]. Another interesting capability of chiral metamaterials is that they can provide negative refractive index for circularly polarized light [22, 23]. This chirality approach for the achievement of negative index is an alternative to the more common approach which requires combination of negative permeability and negative permittivity.
The majority of today’s practically realized metamaterials operate in the microwave part of the electromagnetic spectrum, while there is a great interest and effort to extend their operation regime to higher frequencies, from THz to the optical regime [15, 24, 25]. The extension of metamaterial operation in the THz and far-infrared (IR) regime and the realization of metamaterial-based THz components is a task of undeniable technological importance. This is due to the fact that natural materials do not show strong response to the THz radiation; thus they are not offered for the realization of THz manipulation components, although the technological importance of the THz radiation, especially in domains like imaging, security and sensing is well recognized.
Thus, chiral metamaterials operating in the THz and far-IR regime can provide a valuable tool for the polarization manipulation of THz and far-IR waves. However, not-many attempts to realize and demonstrate THz chiral metamaterials have been made up to now [15, 26–28]. Most of the existing chiral metamaterial structures concern microwave metamaterials, while there are also few studies on optical chiral structures. Those studies have provided a variety of chiral designs that are quite easy to fabricate and show giant optical activity and circular dichroism, as well as negative index of refraction. The majority of the proposed designs are based on the bi-layer configuration, introduced in reference [29], i.e. they are composed of two layers of metallic structures that are not electrically connected; their chiral response comes from their electromagnetic coupling. Such designs enable easy fabrication and size-scaling as to tune the chiral response. Here we follow this approach, of the bi-layer conductor configuration, and demonstrate both theoretically and experimentally various chiral metamaterial structures fabricated on flexible substrates using UV-lithography [24, 30]; the structures operate in THz and show giant optical activity and negative index of refraction for both left- and right-handed circularly polarized waves. Moreover, the proposed designs can be employed to give optically tunable/switchable chiral structures [12, 13]. The optical tunability is achieved by inserting in the structures a photoconducting semiconductor. Actually, there are two main ways/approaches followed so far in order to demonstrate optically switchable chiral metamaterials: Employing a photoconductive substrate [24, 31] (a), and replacing properly-selected metal parts of the structure by a photoconducting semiconductor (b). The second approach, which is followed here, has the advantage that it does not affect the whole spectrum of the metamaterial response but it can control only specific metamaterial resonances [31–33]. Following this approach, we numerically demonstrate here large tunable optical activity and switchable ellipticity response in our planar THz chiral structures by properly inserting into the structures photoconducting silicon.
All the above mentioned studies concern planar chiral structures, having the great advantage that they can be easily fabricated in a layer-by-layer fashion. Such structures though, despite the ease of their fabrication, lack the possibilities offered by fully three-dimensional (3D) volumetric structures, which allow much larger variety of structure designs, more subwavelength scale metamaterial resonators, larger flexibility in the coupling between adjacent resonators (not only electromagnetic coupling but coupling via electric-current connections) and larger structure-incident field coupling possibilities (e.g. both magnetic and electric coupling). Such 3D volumetric structures have become in the recent years possible thanks to quite recently established advanced micro- and nanofabrication approaches, like 3D printing and direct-laser-writing [34–36]. By combining the 3D fabrication possibilities and magnetoelectric coupling (as in chiral structures) with anisotropy, one can achieve even more rich behavior than the one achieved in bi-layer chiral structures. One such possibility which is demonstrated in the present work is asymmetric transmission of linearly polarized waves due to asymmetric coupling of magnetic dipole resonances [34]. This is demonstrated in a 3D volumetric structure based on two perpendicular split-cube resonators (SCRs) [34]. The structure was fabricated by direct laser writing (DLW) [37, 38] and selective silver coating [35, 36], a technique able to provide fully 3D structures with deep-subwavelength resolution, and it operates in middle infra-red (15–40 THz), a frequency region of significant technological interest, where the requirement for EM wave control components is still high, despite substantial recent developments.
2 Planar bi-layer chiral metamaterials
2.1 The designs
The planar bi-layered chiral structures discussed here are shown in Figure 1, while their geometrical features are presented in Table 1 [24]. The first design (Figure 1a) is an assembly of double-layered metallic U-shaped resonators (U-SRRs), where each U-SRR of the upper layer is rotated by 90° in respect to its counterpart of the lower layer. The in-plane unit-cell contains four U-SRRs mutually rotated as to ensure four-fold rotational symmetry of the system. This pair of mutually rotated U-SRRs was first discussed in reference [39] and proposed for the construction of uniaxial chiral structures in reference [40]; it was subsequently studied experimentally in GHz [41], THz [42], and infrared or optical frequency range [43, 44]. It was found that a pure optical activity (i.e. polarization rotation with no ellipticity) as high as 807° per wavelength and 417° per wavelength can occur in the GHz and optical regime, respectively, associated with sufficiently high (more than 40%) transmission. The next two designs are based on the conjugated gammadion structure [45]. They consist of a pair of crosses with Z-type arms, as shown in Figures 1b and 1c. The unit cell of the fourth chiral design of Figure 1 is composed of a pair of silver crosses (cross-wires design) rotated against each other by an angle of φ = 30° (in Figure 1d we show the design as has been modified to give switchable chiral response – see end of the present subsection). A similar design was first studied in GHz range [46], where it showed a pure optical activity as high as 448° per wavelength (at 7 GHz) and negative index of refraction, and subsequently in the optical regime [47], showing optical activity 62° per wavelength (at 220 THz) but no negative index. The last chiral design of Figure 1 (see Figure 1e) consists of a pair of silver squares (square-pairs design) rotated against each other by an angle φ = 25°. It can be considered as arising from the cross-wires design by increasing the wire width to be equal with the wire length.
 |
Figure 1. Schematic of the unit cell of the planar chiral metamaterials under consideration [24]: (a) two relatively rotated layers of four U-SRRs, (b) and (c) two layers of Z-type crosses with φ = 90° and φ = 60°, respectively; the back-layer is the mirror image of the front layer; (d) two relatively rotated layers of cross-wires and (e) design based on two relatively rotated squares. The metal (yellow-color) thickness tm and the dimensions ax, ay, L, w, a, d, φ and s, for each design are presented in Table 1. In Figure 1d grey color corresponds to photoconductive silicon. The wave propagation is along the z direction. |
In all the designs of Figure 1 the conjugated arrangement of the metallic resonators is such as to lead to no center of inversion and no mirror-symmetry plane for the structure, which, in combination with the C4 rotational symmetry of all the designs [45, 48], ensures pure, bi-isotropic chiral response, i.e. that the eigenmodes in all cases are the pure circularly polarized waves.
To physically understand this bi-isotropic chiral response of the designs of Figure 1 one can consider the structures as inherited from the cut-wire-pair structure (see Figure 2a). As is well known in metamaterials community, a pair of cut-wires, as the one shown in Figure 2a, is characterized by a resonant magnetic mode associated with antiparallel currents in the two wires of the pair, and resulting to opposite charges at the facing ends of back and front wire (see Figure 2a). To achieve a bi-isotropic chiral response one needs to displace these opposite charges of the two wires in such a way as to create an electric dipole parallel to the magnetic dipole created by the antiparallel currents. One way to achieve such a displacement is to mutually rotate the wires (see Figure 2b), creating designs like the ones of Figures 1d and 1e. Another way is to add proper extensions at the ends of wires, as shown in Figure 2c, creating designs similar to those of Figures 1b, 1c and 1a.
 |
Figure 2. (a) A pair of metallic cut wires, excited by an incident magnetic field, H, as shown in the figure, exhibits a resonant antisymmetric current mode creating a resonant magnetic dipole, moment, m. The darker yellow color indicates the front-wire the lighter yellow color the back-wire, j is the current density which in the back wire is indicated by a dashed arrow. (b) The wires of panel (a) mutually twisted, and (c) with proper extensions, as to create a dipole moment p, parallel to m. |
Adding another metallic pair to the designs of Figures 2b and 2c, 90° rotated in respect to the first one, one ensures isotropic response in the E-H plane, which is a necessary condition for the eigen-waves to be the circularly polarized waves.
Coming back to the designs of Figure 1, as was mentioned in Section 1 these designs can be employed as to give switchable chiral response. In order to demonstrate here the switchable chirality response, we employed the design shown in Figure 1d; there, in the front cross, parts of the metal have been replaced by photoconducting Si (gray color in Figure 1d), while the back cross remains fully metallic. Proper illumination of the structure by, e.g., a UV laser, changes the Si conductivity, altering the current in the structure and through it its chiral properties.
2.2 Structure fabrication
The fabrication of our chiral structures has been done using UV-lithography, in an alternating layer-by-layer fashion of polyimide and silver. We used a standard spin-on polyimide (DuPont Pyralin SP series PI-2525) with a dielectric constant of 2.9. The sequence of layers starts by spinning and curing a 5 μm thick layer of polyimide on a Si substrate. A silver film (with a thickness tm of 0.5 or 1.0 μm, depending on the design) is deposited on top and patterned by use of standard lift-off techniques. Another layer of polyimide (spacer layer) is spun on over the metallic layer and cured. The thickness of this polyimide layer is 1 μm. Another metal layer is deposited and patterned, while the sequencing of layers continues with another 5 μm thick polyimide layer. The layer-to-layer alignment was done with a Karl Suss MA6 mask aligner and UV photolithography. The alignment accuracy is of the order of 0.5 μm. After the fabrication, the polyimide-encapsulated metallic chiral structures were removed from the Si substrate. The resultant samples are polymer based and flexible, with an area of 15 mm × 15 mm and thickness between 11.8 μm and 13 μm (depending on the design). Further information on the fabrication technique can be found in reference [24].
2.3 Experimental and numerical electromagnetic characterization approach
The experimental EM characterization of the planar chiral samples (see Figure 1) was performed in the frequency regime 2–12 THz, which is below the polyimide absorption bands (~12 THz and ~20 THz). The experimental characterization was done through transmission measurements, which were performed using a Bruker IFS 66v/S Fourier-transform infrared spectrometer (with a collimated beam) and two linear polyethylene grid polarizers [24].
The results of the measurements were compared in all cases with corresponding simulations. For the simulations we used a commercial three-dimensional full-wave solver (CST Microwave Studio, Computer Simulation Technology GmbH, Darmstadt, Germany) based on the Finite Element Method. We considered in the simulations a single unit cell, as shown in Figure 1, with periodic boundary conditions along x and y directions, while an incident plane wave propagating along z-direction was used to excite the structure. For modeling the metallic parts of the structure (silver; yellow color in Figure 1) we considered a lossy-metal model with a conductivity of σAg = 5.71 × 106 S/m, in agreement with previous conductivity measurements [36]. For the photoactive silicon areas (marked in grey in Figure 1 and with geometrical features mentioned in Table 1) which replace parts of the metal of the front metal-layer, we applied a simple conductivity model, considering εSi = 11.9, and conductivity, σSi, varying from 2.5 × 10−4 S/m (corresponding to no illumination, i.e. insulating Si) to 1 × 105 S/m [32], which is the maximum recorded conductivity achieved experimentally by means of optical pumping, using a 30-fs laser system at 800 nm central wavelength [13, 31, 33, 49, 50].
2.4 Chiral structures response
In this section, the chiral behavior of the structures shown in Figure 1 will be discussed. Figure 3 shows the transmission results for those structures, obtained by both simulations and experiments, for linearly polarized incident waves. In general one needs to measure or calculate four transmission components, Txx, Txy, Tyx and Tyy, where the first and second subscript indicate the output and input signal polarizations, respectively; e.g.  is the input y-polarized electric field and
is the input y-polarized electric field and  is the transmitted x-polarized electric field [14, 15]. Due to the four-fold rotational symmetry of our structures Txx = Tyy and Txy = −Tyx [16], so only two transmission amplitudes, e.g. Txx and Txy, are needed to be considered and those are presented in Figure 3.
is the transmitted x-polarized electric field [14, 15]. Due to the four-fold rotational symmetry of our structures Txx = Tyy and Txy = −Tyx [16], so only two transmission amplitudes, e.g. Txx and Txy, are needed to be considered and those are presented in Figure 3.
 |
Figure 3. Simulated (left column) and measured (right column) magnitude of the transmission components (Txx: solid lines, Txy: dashed lines), for the fully metallic planar chiral metamaterials presented in Figure 1, and for linearly polarized incident wave [24]. The insets show the corresponding designs. |
In the results of Figure 3, besides the very good quantitative agreement between simulations and experiments, one can observe a slight broadening of the resonance dips in the experimental cases (compared to the theory) due to the non-uniformity in the fabrication of the samples.
As can be observed in Figures 3a and 3f, the U-SRR structure shows two distinct resonances. This is in agreement with the discussion of reference [41], where the resonances and the associated current modes are described in detail.
Observing the response of the structures of Figures 3b, 3g, 3c and 3h, one can see a more complicated spectrum with more resonances in Txx and larger cross-polarized transmission levels, indicating larger optical activity, as already discussed in reference [24].
The structure of Figures 3d and 3i, as was mentioned also in Section 2.1, has been studied both in GHz and the optical regime. There, it showed two distinct low-frequency resonances which were classified as “magnetic” (the lower one – associated with antiparallel currents in the equivalent branches of the pair) and “electric” (the higher frequency one – associated with parallel currents in the equivalent branches of the pair). The absence of these two distinct resonances in our case is due to the fact that these resonances in our particular geometry lie very close to each other, being thus merged in a single Fano-type transmission peak. One way to avoid this merging and move the electric dipole-like resonance well above the magnetic one in a cut-wire-pair system is to make the wires wider [51], taking the form of slabs. This is verified in the case of Figures 3e and 3j, where the wires of Figures 3d and 3i have been replaced by square slabs and the double-resonance picture has been regained.
As was mentioned earlier, high cross-polarized transmission values are indications of large optical activity of the corresponding structures. To confirm this large optical activity and to fully evaluate the chiral response of a structure one needs though to obtain the transmission for circularly polarized waves. This can be easily calculated from the transmission for linearly polarized waves, employing the formula (1)
(1)
Equation (1) in our case, due to four-fold rotational symmetry of the structures, can be simplified to T++ = Txx + iTxy, T−− = Txx − iTxy, T+− = T−+ = 0, where the subscript + denotes the right-handed circularly polarized wave (RCP) and the subscript − the left-handed circularly polarized wave (LCP), while the first subscript again indicates the polarization of the transmitted wave and the second the polarization of the incident wave.
From the circular polarization transmission components one can obtain the optical activity, θ, of a structure (defined as the angle between the major axis of the polarization ellipse of the transmitted wave and the polarization of the incident wave) and the ellipticity angle, η, of the transmitted wave (resulting from the circular dichroism, i.e. the absorption difference between left and right handed transmitted waves) according to the equations![$$ \theta =\frac{1}{2}\left[\mathrm{arg}\left({T}_{++}\right)-\mathrm{arg}\left({T}_{--}\right)\right],\eta =\frac{1}{2}\mathrm{si}{\mathrm{n}}^{-1}\left(\frac{{\left|{T}_{++}\right|}^2-{\left|{T}_{--}\right|}^2}{{\left|{T}_{++}\right|}^2+{\left|{T}_{--}\right|}^2}\right). $$](/articles/epjam/full_html/2015/01/epjam150019/epjam150019-eq4.gif) (2)
(2)
In our case, since the simulated transmission results are in very good agreement with the corresponding measurement results, we based the circularly polarized transmitted wave calculations to the simulated linear transmissions, where phase information is also available.
One of the particularly desired features of a chiral structure is to give large optical activity associated with negligible ellipticity (and high transmittance); this corresponds to pure rotation of a linearly polarized incident wave while maintaining its linear polarization character. The maximum pure optical activity values achievable in the structures of Figure 1 are presented in Table 2, together with the associated transmission levels. As can be seen in Table 2, all the structures can give quite high pure optical activity values, which make them suitable for a variety of polarization manipulation applications.
Another desired feature of a chiral structure is the achievement of quite large ellipticity (resulting from large circular dichroism), enabling the realization of circular polarizers. In this respect the structure of Figure 1a is superior compared to the other structures of Figure 1, as it gives ellipticity values of 45° with more than 70% transmittance.
Finally, another merit of the designs of Figure 1 is that they all present quite broad frequency regions of negative refractive index response, as well as regions with refractive index close to zero. Both the negative and the near zero refractive index are associated with unusual and unique metamaterial phenomena (e.g. negative refraction and backward propagation for the negative index [3], beam collimation, squeezing, static-like optical fields etc. for the near-zero index [4, 52]).
2.5 Switchable chirality response
As was mentioned in Section 1, one way to optically modulate the chiral response of a structure is to insert properly in the structure unit cell a photoconducting semiconductor, which can be transformed from an insulator to a conductor state via photoexcitation, altering thus the current in the structure and through it its chiral response. We demonstrate here the potential for optically controllable response of our structures employing the design of Figure 1d, where parts of the front-metallic cross have been replaced by Si (grey color in Figure 1d) – the back cross remains fully metallic. In Figure 4 we present the simulated transmission amplitudes |Txx| (upper panel) and |Txy| (lower panel) for different Si conductivity values, including the case of full silver cross shown also in Figure 3 (for comparison), demonstrating a Fano-type resonance around 5.5 THz. Decreasing the Si conductivity from that of silver, the front-cross gradually becomes a mini-one, and the original Fano-like resonance observed in the full-metal case splits into two distinct resonances: the lower-frequency one is predominantly due to the dipole-like response of the back cross and the higher one, at ~8.8 THz, corresponds to the dipole-like resonance of the front mini-cross (but slightly modified from the interaction of the crosses). The current distributions at each resonance for σSi = 1 × 103 S/m are shown in the bottom panel of Figure 4, demonstrating that at each resonance frequency only one of the crosses is strongly excited [32].
 |
Figure 4. Simulated transmission amplitudes |Txx| (upper panels) and |Txy| (lower panels), for the chiral metamaterials shown in Figure 1d, for linearly polarized incident wave [32]. One can see the cases of silver (black lines) and photoconductive silicon with σSi = 1 × 105 S/m (red lines) or 1 × 103 S/m (green lines) or 2.5 × 10−4 S/m (blue lines), respectively. The bottom panel shows the corresponding current distributions at the resonance frequencies for σSi = 1 × 103 S/m with Ey linearly polarized incident wave. |
Employing the linear transmission data shown in Figure 4 we calculated the circular transmission components and through them the optical activity of the structure and the transmitted wave ellipticity for different values of the Si conductivity. The results are shown in Figure 5.
 |
Figure 5. Simulated optical activity, θ (solid lines), and ellipticity, η (dashed lines), for the switchable chiral structure under consideration [32]. One can see the cases of silver (black lines) and photoconductive silicon with σSi = 1 × 105 S/m (red lines) or 1 × 103 S/m (green lines) or 2.5 × 10−4 S/m (blue lines), respectively. The inset shows the corresponding design in which grey color corresponds to photoconductive silicon and yellow corresponds to metal (silver). |
Figure 5 clearly demonstrates the notable tunable optical activity and switchable ellipticity response of the structure. In the region around 5.5 THz the structure can be easily switched from circular to linear polarizer by changing the flux of the excitation power. Similar switchable response is observed also at ~8.8 THz. Examining in detail the ellipticity features for every planar chiral design presented in Figure 1 [32], one can conclude that there is an optimum conductivity (σSi = 1 × 105 S/m) which produces in many cases an impressive maximum in ellipticity, reaching almost ±45° (i.e. ~100% transformation of an incoming linearly polarized into a circularly polarized transmitted wave) [32], demonstrating the switchable polarizer capabilities of our designs.
3 Three-dimensional bi-anisotropic metamaterials
Although the pure bi-isotropic chiral designs, where the eigenmodes are circularly polarized waves, can show in many cases impressive polarization control capabilities, one can achieve even more impressive phenomena and possibilities in “anisotropic chiral” designs, i.e. structures combining anisotropy with magnetoelectric coupling [8]. Moreover, going from planar designs to fully 3D bulk structures one can gain additional design and thus novel property engineering possibilities. In this part of the paper we present a design combining all the above merits. This design, which can be easily fabricated by direct laser writing [34, 35, 37], besides its strong optical activity response shows also large asymmetric transmission response, i.e. different transmittance for waves incident from two opposite sides of a structure sample [53–57]. This gives to the structures the ability to be used in polarization isolation related applications.
3.1 The design
The unit cell of the 3D metamaterial design employed in the present study is shown in Figure 6. It consists of two split-cube resonator (SCR) structures rotated by 90° with respect to each other along the z- (propagation) direction [34]. The geometrical structure parameters for the structure as fabricated and characterized experimentally are detailed in the caption of Figure 6. As can be seen from Figure 6, the structure lacks mirror symmetry along all x, y, z directions as well as C4 rotational symmetry in the x-y plane.
 |
Figure 6. (a) Schematic of the unit cell of the 3D SCR metamaterials under consideration [34]. The dimensions of the fabricated structure are ax = ay = 8.0 μm, az = 9.1 μm, w1 = 600 nm, and w2 = 850 nm, respectively. The wave propagation is along the z direction. (b) Top view of SEM image of the 3D SCR metamaterial, recorded at 15 kV. The magnification scale can be seen below the SEM image. |
The Split Cube Resonator (SCR), which is the basic structure element, exhibits both the electric and the magnetic response of the most common metamaterial elements. Its electric response, for electric field parallel to the cube axis, is similar to that of a long wire [58], while its magnetic response, for magnetic field parallel to the cube axis, is that of a split ring resonator (SRR) [59]. Combining two perpendicular SCRs in the unit cell one can in principle achieve both the electric response of the wires and the magnetic response of the SRRs. If the two SCRs though are conductively coupled, this coupling results to more complex response than just the response coming from the addition of SRRs and wires. It results to different response for linearly polarized waves incident from opposite illumination directions. In particular the excitation of a resonant magnetic moment in the first SCR excites a resonant magnetic response in the second SCR, producing large cross polarized (and small co-polarized) transmission. If the incident magnetic field direction is such that does not allow magnetic excitation of the first SCR, the wave is just reflected due to negative permittivity response of the parallel to the applied electric field cubes. This results to strong asymmetric transmission for linearly polarized waves, as well as strong polarization conversion.
3.2 Metamaterial fabrication and electromagnetic characterization
As was mentioned in the Introduction, the 3D structure was discussed here fabricated by Direct Laser Writing (DLW) followed by electroless silver plating. DLW by multi-photon polymerization is a 3D printing technology that allows the fabrication of 3D structures with resolution below 100 nm. Briefly, the beam of an ultra-fast laser is tightly focused inside the volume of a transparent and photosensitive monomer, causing it to absorb two or more photons and polymerize locally. By moving the beam in three dimensions inside the photopolymer volume, one can fabricate 3D structures of great accuracy. The photosensitive material used for the fabrication is an organic-inorganic composite, produced by the addition of Methacryloxypropyl Trimethoxysilane (MAPTMS) to Zirconium n-Propoxide. 2-(dimethylamino)ethyl methacrylate (DMAEMA), acting as a metal-binding moiety, was also added and copolymerized with MAPTMS upon photopolymerization. Michler’s ketone (4,4-bis(diethylamino) benzophenone, BIS) was used as the photoinitiator. The structure was fabricated on a glass substrate. Further information on the fabrication technique and the photosensitive material synthesis can be found in reference [34].
The experimental electromagnetic characterization of the structure was performed in the frequency region 15–40 THz, through reflection measurements, performed using a Bruker Vertex 70v Fourier-transform infrared spectrometer with a collimated beam, attached to a Bruker Hyperion 2000 infrared microscope and two linear ZnSe grid polarizers [34]. The experimental results were compared in all cases with corresponding simulation data, obtained with CST Microwave Studio, as described in Section 2.3.
3.3 Asymmetric transmission and polarization transformer response
Since the 3D SCR structure was fabricated on glass, which is not transparent in the far infrared region of interest, we characterized the structure experimentally by measuring the reflection rather than the transmission coefficients [34]. Thus, for linearly polarized incident waves four reflection components were measured: Rxx, Rxy, Ryx and Ryy [34]. These reflection components were in very good quantitative agreement with the corresponding simulations, allowing us to rely on the simulations in order to analyze the structure performance and properties. Calculating the transmission components for the structure, we obtained the results presented in Figure 7a, showing the components Txx, Tyy, Txy, Tyx (absolute values) for waves propagating along the positive z-direction in the 3D SCR structure. Using these components we calculated and show in Figure 7b the total transmitted field amplitudes for x and y incident wave polarizations,  and
and  , respectively [34].
, respectively [34].
 |
Figure 7. (a) Simulated transmission components (absolute values) for linearly polarized incident waves propagating through the 3D SCR structure along the forward (positive) z-direction [34]. The red solid curve coincides with the blue solid curve. (b) Total transmitted amplitude for x- and y-polarized incident wave, |
Asymmetric transmission, Δ, is the difference in the transmittance (transmitted intensity divided by the incident intensity) for waves propagating along two opposite directions (in our case the forward (positive) and backward (negative) z-direction), i.e. (3)
(3)
where the superscripts f and b denote the forward and backward z-direction respectively. Taking into account the symmetry of our structure and the relation between backward and forward transmission components for reciprocal media  , one can see that the transmittance of an x-polarized incident wave propagating along the backward (negative) z-direction is equal to the transmittance of a y-polarized incident wave propagating along the forward z-direction, i.e.
, one can see that the transmittance of an x-polarized incident wave propagating along the backward (negative) z-direction is equal to the transmittance of a y-polarized incident wave propagating along the forward z-direction, i.e. ; thus instead of inverting the incidence direction for calculating the asymmetric transmission Δ, one can change the incident wave polarization. Therefore, for a x-polarized incident wave [34]
; thus instead of inverting the incidence direction for calculating the asymmetric transmission Δ, one can change the incident wave polarization. Therefore, for a x-polarized incident wave [34] (4)
(4)
i.e. the asymmetric transmission becomes equal to the difference of the cross-polarized transmitted intensities for x- and y-incident wave polarizations.
As can be seen in Figure 7a the cross-polarized transmission amplitudes Tyx and Txy are quite different, especially in the region centered at 21.5 THz, indicating strong asymmetric transmission. This strong asymmetric transmission for frequencies between 21 and 22 THz is demonstrated clearly in Figure 7b where the total transmission is shown [34].
From Figure 7b one could note that, contrary to most of the structures discussed so-far in the literature, the asymmetric transmission band here at around 21.5 THz appears as pass-band imposed in a broad region of forbidden propagation and transmission (from zero to ~28 THz). This broad stop-band is due to a negative permittivity response provided by the metallic cubes which are parallel to the incident electric field direction (the metallic cubes act as a wire-grid-polarizer), resulting to small co-polarized transmission amplitudes |Txx| and |Tyy|, as shown in Figure 7a [34]. The transmission band around 21.5 THz (i.e. the asymmetric transmission band) is due to a magnetic resonance of the parallel to the external magnetic field cubes, coupled to the equivalent magnetic resonance of the perpendicular cubes, and superimposed to the negative permittivity response of the cubes. (The double-peak character of that band is a result of the mode-splitting due to this magnetic resonance coupling.)
From the results of Figure 7b one can also see that in the asymmetric transmission band around 21.5 the structure looks quite transparent along one propagation direction and quite opaque if “seen” from the opposite direction for illumination with a linearly polarized wave polarized along one of the principal lattice directions [34]. This “low” versus “high” transmittance (which results from the large difference between |Txy| and |Tyx| combined with the small values of the co-polarized transmission amplitudes |Txx| and |Tyy| [34, 60]) is a highly desired feature in polarization control and isolation applications.
To fully characterize the polarization control capabilities of the 3D SCR structure we further analyzed the transmission results to obtain the optical activity and the transmitted wave ellipticity. Since in this case the eigenwaves of the structure are not the circularly polarized waves (i.e. T+− and T−+ are not zero), for the calculation of the optical activity and ellipticity one cannot apply the formulas of equation (2). We rather calculated these quantities taking into account the Stokes Parameters [61] and the approach by Bassiri et al. [62] (see also Supplementary material of Ref. [34]). The results are shown in Figure 8.
 |
Figure 8. Simulated optical activity, θ (blue solid line), and ellipticity, η, (red dashed line) for the wave transmitted through the 3D SCR metamaterials under consideration, when the metamaterial is excited by a x-polarized incident wave (Figure 6a) propagating along the forward z-direction [34]. |
Figure 8 depicts the optical activity and the ellipticity when the metamaterial is excited by a x-polarized incident wave propagating along the forward z-direction [34] (for the same wave propagating along the backward z-direction the transmission is close to zero, so there is no meaning to speak about polarization control via transmission). Analyzing the response of our structure at the asymmetric transmission band at ~21.5 THz by examining the results of Figures 7a and 8, one can see that a x-polarized incident wave is almost totally transformed to y-polarized wave when passing through the structure [34]. This indicates a close to 90° “one-way” optical activity of the structure, validating the potential of the structure to be used as a 90° one-way polarization converter [34].
4 Conclusions
The current work demonstrates the polarization control capabilities offered by different THz and far-IR chiral designs both isotropic and anisotropic. Regarding isotropic designs we were focused on structures based on the bi-layer conductor configuration; we analyzed, both theoretically and experimentally, different structures, all showing quite large optical activity, significant circular dichroism and negative index of refraction response in the THz region, making them promising elements for the realization of THz wave manipulation components and systems. Moreover, we demonstrated theoretically the potential of some of those designs to give tunable and switchable components, replacing parts of the metallic structures by photoconducting silicon and demonstration (through simulations) the switchable and tunable chirality response of the structures by changing the silicon conductivity, employing conductivity values corresponding to various, practically achievable, photoexcitation intensities. The prominent tuning capabilities of the proposed structures, along with their simplicity, which allows their easy fabrication and scaling towards optical frequencies, and the possibility to be fully flexible (since they are encapsulated in polyimide), makes them important candidate for the realization of both passive and active THz polarization manipulation components like polarization filters, modulators, wave-plates, etc. [32].
Regarding anisotropic designs, we studied theoretically and experimentally the asymmetric transmission properties and the polarization control capabilities of a novel 3D infra-red metamaterial structure obtained by employing direct laser writing and selective silver coating. The experimental study was done through reflection measurements while associated transmission and reflection simulations revealed quite large asymmetric transmission for linearly polarized waves, and 90° one-way pure optical activity. The achievement of these nice asymmetric-transmission-related properties of the structure is due to the combination of both electric and magnetic responses of the SCRs, and offers additionally the possibility of impedance control (adjusting thus the asymmetric transmission values), and of “one-way” backward propagation.
Acknowledgments
This work was supported by Greek GSRT project ERC02-EXEL, and by the European Research Council under ERC Advanced Grant No. 32081 (PHOTOMETA). Work at Ames Laboratory was partially supported by the Department of Energy (Basic Energy Sciences, Division of Materials Sciences and Engineering) under Contract No. DE-AC02-07CH11358 (computational studies). Authors acknowledge the contribution of all co-authors of Refs. [24, 32, 34]. Author M. K. acknowledges also useful discussions with Prof. Sergei Tretyakov.
References
- C.M. Soukoulis, M. Kafesaki, E.N. Economou, Negative index materials: new frontiers in optics, Adv. Mat. 18 (2006) 1941–1952. [CrossRef] [Google Scholar]
- Y. Liu, X. Zhang, Metamaterials: a new frontier of science and technology, Chem. Soc. Rev. 40 (2011) 2494–2507. [Google Scholar]
- V.G. Veselago, The electrodynamics of substances with simultaneously negative values of ε and μ, Sov. Phys. Usp. 10 (1968) 509–514. [CrossRef] [Google Scholar]
- N. Engheta, Pursuing near-zero response, Science 340 (2013) 286–287. [CrossRef] [Google Scholar]
- M.G. Silveirinha, N. Engheta, Theory of supercoupling, squeezing wave energy, and field confinement in narrow channels and tight bends using epsilon near-zero metamaterials, Phys. Rev. B 76 (2007) 245109. [CrossRef] [Google Scholar]
- A. Poddubny, I. Iorsh, P. Belov, Y. Kivshar, Hyperbolic metamaterials, Nat. Photonics 7 (2013) 10. [Google Scholar]
- N.I. Zheludev, Y.S. Kivshar, From metamaterials to metadevices, Nat. Mater. 11 (2012) 917–924. [CrossRef] [Google Scholar]
- A. Sihvola, Metamaterials in electromagnetics, Metamaterials 1 (2007) 2–11. [CrossRef] [Google Scholar]
- J.K. Gansel, M. Thiel, M.S. Rill, M. Decker, K. Bade, V. Saile, G.V. Freymann, S. Linden, M. Wegener, Gold helix photonic metamaterial as broadband circular polarizer, Science 325 (2009) 1513–1515. [CrossRef] [PubMed] [Google Scholar]
- J.J.D.D. Jong, L.N. Lucas, R.M. Kellogg, J.H.V. Esch, B.L. Feringa, Reversible optical transcription of supramolecular chirality into molecular chirality, Science 304 (2004) 278–281. [CrossRef] [Google Scholar]
- M. Wegener, S. Linden, Giving light yet another new twist, Physics 2 (2009) 3–6. [CrossRef] [Google Scholar]
- S. Zhang, J. Zhou, Y. Park, J. Rho, R. Singh, S. Nam, A.K. Azad, H. Chen, X. Yin, A.J. Taylor, X. Zhang, Photoinduced handedness switching in terahertz chiral metamolecules, Nat. Commun. 3 (2012) 3–6. [Google Scholar]
- J. Zhou, D.R. Chowdhury, R. Zhao, A.K. Azad, H. Chen, C.M. Soukoulis, A.J. Taylor, J.F. O’Hara, Terahertz chiral metamaterials with giant and dynamically tunable optical activity, Phys. Rev. B 86 (2012) 035448. [CrossRef] [Google Scholar]
- B. Wang, J. Zhou, T. Koschny, C.M. Soukoulis, Nonplanar chiral metamaterials with negative index, Appl. Phys. Lett. 94 (2009) 151112. [CrossRef] [Google Scholar]
- Z. Li, M. Mutlu, E. Ozbay, From optical activity and negative refractive index to asymmetric transmission, J. Opt. 15 (2013) 023001. [CrossRef] [Google Scholar]
- B.N. Wang, J.F. Zhou, T. Koschny, M. Kafesaki, C.M. Soukoulis, Chiral metamaterials: simulations and experiments, J. Opt. A: Pure Appl. Opt. 11 (2009) 114003. [CrossRef] [Google Scholar]
- K. Murata, M. Aoki, T. Suzuki, T. Harada, H. Kawabata, T. Komori, F. Ohseto, K. Ueda, S. Shinkai, Thermal and light control of the sol-gel phase transition in cholesterol-based organic gels. Novel helical aggregation modes as detected by circular dichroism and electron microscopic observation, J. Am. Chem. Soc. 116 (1994) 6664–6676. [CrossRef] [Google Scholar]
- N. Koumura, R.W.J. Zijlstra, R.A.V. Delden, N. Harada, B.L. Feringa, Light-driven monodirectional molecular rotor, Nature 401 (1999) 152–155. [CrossRef] [PubMed] [Google Scholar]
- R. Zhao, J. Zhou, T. Koschny, E.N. Economou, C.M. Soukoulis, Repulsive Casimir force in chiral metamaterials, Phys. Rev. Lett. 103 (2009) 103602. [CrossRef] [PubMed] [Google Scholar]
- R. Zhao, T. Koschny, E.N. Economou, C.M. Soukoulis, Repulsive Casimir forces with finite-thickness slabs, Phys. Rev. B 83 (2011) 075108. [CrossRef] [Google Scholar]
- G. Kenanakis, C.M. Soukoulis, E.N. Economou, Casimir forces of metallic microstructures into cavities, Phys. Rev. B 92 (2015) 075430. [CrossRef] [Google Scholar]
- J.B. Pendry, A chiral route to negative refraction, Science 306 (2004) 1353–1355. [CrossRef] [PubMed] [Google Scholar]
- S. Tretyakov, A. Sihvola, L. Jylha, Bi-layer cross chiral structure with strong optical activity and negative index, Photonics Nanostruct. Fundam. Appl. 3 (2005) 107–115. [CrossRef] [Google Scholar]
- G. Kenanakis, R. Zhao, A. Stavrinidis, G. Konstantinidis, N. Katsarakis, M. Kafesaki, C.M. Soukoulis, E.N. Economou, Flexible chiral metamaterials in the terahertz regime: a comparative study of various designs, Opt. Mater. Express 2 (2012) 1702–1712. [CrossRef] [Google Scholar]
- C.M. Soukoulis, M. Wegener, Past achievements and future challenges in the development of three-dimensional photonic metamaterials, Nat. Photonics 5 (2011) 523–530. [Google Scholar]
- Y. Huang, Z. Yao, Q. Wang, F. Hu, X. Xu, Coupling Tai Chi chiral metamaterials with strong optical activity in terahertz region, Plasmonics 10 (2015) 1005–1011. [CrossRef] [Google Scholar]
- E.V. Naumova, V.Y. Prinz, S.V. Golod, V.A. Seleznev, R.A. Soots, V.V. Kubarev, Manufacturing chiral electromagnetic metamaterials by directional rolling of strained heterofilms, J. Opt. A: Pure Appl. Opt. 11 (2009) 074010. [CrossRef] [Google Scholar]
- N. Wongkasem, A. Akyurtlu, K.A. Marx, D. Qi, L. Jin, W.D. Goodhue, Development of chiral negative refractive index metamaterials for the terahertz frequency regime, IEEE Trans. Antennas Propag. 55 (2007) 3052–3062. [CrossRef] [Google Scholar]
- E. Plum, V.A. Fedotov, A.S. Schwanecke, N.I. Zheludev, Y. Chen, Giant optical gyrotropy due to electromagnetic coupling, Appl. Phys. Lett. 90 (2007) 223113. [CrossRef] [Google Scholar]
- A. Sonsilphong, P. Gutruf, W. Withayachumnankul, D. Abbott, M. Bhaskaran, S. Sriram, N. Wongkasem, Flexible bi-layer terahertz chiral metamaterials, J. Opt. 17 (2015) 085101. [CrossRef] [Google Scholar]
- M. Kafesaki, N.H. Shen, S. Tzortzakis, C.M. Soukoulis, Optically switchable and tunable terahertz metamaterials through photoconductivity, J. Opt. 14 (2012) 114008. [CrossRef] [Google Scholar]
- G. Kenanakis, R. Zhao, N. Katsarakis, M. Kafesaki, C.M. Soukoulis, E.N. Economou, Optically controllable THz chiral metamaterials, Opt. Express 22 (2014) 12149–12159. [CrossRef] [Google Scholar]
- N.H. Shen, M. Massaouti, M. Gokkavas, J.M. Manceau, E. Ozbay, M. Kafesaki, T. Koschny, S. Tzortzakis, C.M. Soukoulis, Optically implemented broadband blueshift switch in the terahertz regime, Phys. Rev. Lett. 106 (2011) 037403. [CrossRef] [PubMed] [Google Scholar]
- G. Kenanakis, A. Xomalis, A. Selimis, M. Vamvakaki, M. Farsari, M. Kafesaki, C.M. Soukoulis, E.N. Economou, Three-dimensional infrared metamaterial with asymmetric transmission, ACS Photonics 2 (2015) 287–294. [CrossRef] [Google Scholar]
- K. Terzaki, N. Vasilantonakis, A. Gaidukeviciute, C. Reinhardt, C. Fotakis, M. Vamvakaki, M. Farsari, 3D conducting nanostructures fabricated using direct laser writing, Opt. Mater. Express 1 (2011) 586–597. [CrossRef] [Google Scholar]
- N. Vasilantonakis, K. Terzaki, I. Sakellari, V. Purlys, D. Gray, C.M. Soukoulis, M. Vamvakaki, M. Kafesaki, M. Farsari, Three-dimensional metallic photonic crystals with optical bandgaps, Adv. Mater. 24 (2012) 1101–1105. [CrossRef] [Google Scholar]
- M. Farsari, B.N. Chichkov, Two-photon fabrication, Nature Photon. 3 (2009) 450–452. [CrossRef] [Google Scholar]
- M. Malinauskas, M. Farsari, A. Piskarskas, S. Juodkazis, Ultrafast laser nanostructuring of photopolymers: a decade of advances, Phys. Rep. 2013 (2013) 1–31. [CrossRef] [Google Scholar]
- N. Liu, H. Giessen, Three-dimensional optical metamaterials as model systems for longitudinal and transverse magnetic coupling, Opt. Express 16 (2008) 21233–21238. [CrossRef] [Google Scholar]
- R. Zhao, T. Koschny, E.N. Economou, C.M. Soukoulis, Comparison of chiral metamaterial designs for repulsive Casimir force, Phys. Rev. B 81 (2010) 235126. [CrossRef] [Google Scholar]
- Z. Li, R. Zhao, T. Koschny, M. Kafesaki, K.B. Alici, E. Colak, H. Caglayan, E. Ozbay, C.M. Soukoulis, Chiral metamaterials with negative refractive index based on four “U” split ring resonators, Appl. Phys. Lett. 97 (2010) 081901. [CrossRef] [Google Scholar]
- W.-H. Sun, Y.-J. Bao, M. Wang, R.-W. Peng, C. Sun, X. Lu, J. Shao, Z.-F. Li, N.-B. Ming, Construction of a chiral metamaterial with a U-shaped resonator assembly, Phys. Rev. B 81 (2010) 075119. [CrossRef] [Google Scholar]
- M. Decker, R. Zhao, C.M. Soukoulis, S. Linden, M. Wegener, Twisted split-ring-resonator photonic metamaterial with huge optical activity, Opt. Lett. 35 (2010) 1593–1595. [CrossRef] [Google Scholar]
- Y.-P. Jia, Y.-L. Zhang, X.-Z. Dong, M.-L. Zheng, Z.-S. Zhao, X.-M. Duan, Tunable dual-band infrared chiral metamaterials based on double-layered asymmetric U-shape split ring resonators, Physica E 74 (2015) 659–664. [CrossRef] [Google Scholar]
- R. Zhao, L. Zhang, J. Zhou, T. Koschny, C.M. Soukoulis, Conjugated gammadion chiral metamaterial with uniaxial optical activity and negative refractive index, Phys. Rev. B 83 (2011) 035105. [CrossRef] [Google Scholar]
- J. Zhou, J. Dong, B. Wang, T. Koschny, M. Kafesaki, C.M. Soukoulis, Negative refractive index due to chirality, Phys. Rev. B 79 (2009) 121104(R). [CrossRef] [Google Scholar]
- M. Decker, M. Ruther, C.E. Kriegler, J. Zhou, C.M. Soukoulis, S. Linden, M. Wegener, Strong optical activity from twisted-cross photonic metamaterials, Opt. Lett. 34 (2009) 2501–2503. [CrossRef] [Google Scholar]
- C. Menzel, C. Rockstuhl, F. Lederer, Advanced Jones calculus for the classification of periodic metamaterials, Phys. Rev. A 82 (2010) 053811. [CrossRef] [Google Scholar]
- J. Gu, R. Singh, A.K. Azad, J. Han, A.J. Taylor, J.F. O’Hara, W. Zhang, An active hybrid plasmonic metamaterial, Opt. Mater. Express 2 (2012) 31–37. [CrossRef] [Google Scholar]
- H.T. Chen, J.F. O’Hara, A.K. Azad, A.J. Taylor, R.D. Averitt, D.B. Shrekenhamer, W.J. Padilla, Experimental demonstration of frequency-agile terahertz metamaterials, Nat. Photonics 2 (2008) 295–298. [CrossRef] [Google Scholar]
- M. Kafesaki, I. Tsiapa, N. Katsarakis, T. Koschny, C.M. Soukoulis, E.N. Economou, Left-handed metamaterials: the fishnet structure and its variations, Phys. Rev. B 75 (2007) 235114. [CrossRef] [Google Scholar]
- A.M. Mahmoud, N. Engheta, Wave-matter interactions in epsilon-and-mu-near-zero structures, Nature Commun. 5 (2014) 5638. [CrossRef] [Google Scholar]
- V.A. Fedotov, P.L. Mladyonov, S.L. Prosvirnin, A.V. Rogacheva, Y. Chen, N.I. Zheludev, Asymmetric propagation of electromagnetic waves through a planar chiral structure, Phys. Rev. Lett. 97 (2006) 167401. [CrossRef] [Google Scholar]
- C. Menzel, C. Helgert, C. Rockstuhl, E.-B. Kley, A. Tünnermann, T. Pertsch, F. Lederer, Asymmetric transmission of linearly polarized light at optical metamaterials, Phys. Rev. Lett. 104 (2010) 253902. [CrossRef] [Google Scholar]
- A.S. Schwanecke, V.A. Fedotov, V.V. Khardikov, S.L. Prosvirnin, Y. Chen, N.I. Zheludev, Nanostructured metal film with asymmetric optical transmission, Nano Lett. 8 (2008) 2940–2943. [CrossRef] [PubMed] [Google Scholar]
- M. Mutlu, A.E. Akosman, A.E. Serebryannikov, E. Ozbay, Asymmetric transmission of linearly polarized waves and polarization angle dependent wave rotation using a chiral metamaterial, Opt. Express 19 (2011) 14290–14299. [CrossRef] [Google Scholar]
- M. Kang, J. Chen, H.-X. Cui, Y. Li, H.-T. Wang, Asymmetric transmission for linearly polarized electromagnetic radiation, Opt. Express 19 (2011) 8347–8356. [CrossRef] [Google Scholar]
- J.B. Pendry, A.J. Holden, D.J. Robbins, W.J. Stewart, Low frequency plasmons in thin wire structures, J. Phys.: Condens. Matter 10 (1998) 4785–4809. [Google Scholar]
- J. Pendry, A. Holden, D. Robbins, W. Stewart, Magnetism from conductors and enhanced nonlinear phenomena, IEEE Trans. Microwave Theory Tech. 47 (1999) 2075–2084. [Google Scholar]
- Z. Li, M. Mutlu, E. Ozbay, Highly asymmetric transmission of linearly polarized waves realized with a multilayered structure including chiral metamaterials, J. Phys. D: Appl. Phys. 47 (2014) 075107. [CrossRef] [Google Scholar]
- C.H. Papas, Theory of electromagnetic wave propagation, McGraw-Hill, New York, 1965. [Google Scholar]
- S. Bassiri, C.H. Papas, N. Engheta, Electromagnetic wave propagation through a dielectric-chiral interface and through a chiral slab, J. Opt. Soc. Am. A 5 (1988) 1450–1459. [CrossRef] [Google Scholar]
Cite this article as: Kenanakis G, Economou EN, Soukoulis CM & Kafesaki M: Controlling THz and far-IR waves with chiral and bianisotropic metamaterials. EPJ Appl. Metamat. 2015, 2, 15.
All Tables
All Figures
 |
Figure 1. Schematic of the unit cell of the planar chiral metamaterials under consideration [24]: (a) two relatively rotated layers of four U-SRRs, (b) and (c) two layers of Z-type crosses with φ = 90° and φ = 60°, respectively; the back-layer is the mirror image of the front layer; (d) two relatively rotated layers of cross-wires and (e) design based on two relatively rotated squares. The metal (yellow-color) thickness tm and the dimensions ax, ay, L, w, a, d, φ and s, for each design are presented in Table 1. In Figure 1d grey color corresponds to photoconductive silicon. The wave propagation is along the z direction. |
| In the text | |
 |
Figure 2. (a) A pair of metallic cut wires, excited by an incident magnetic field, H, as shown in the figure, exhibits a resonant antisymmetric current mode creating a resonant magnetic dipole, moment, m. The darker yellow color indicates the front-wire the lighter yellow color the back-wire, j is the current density which in the back wire is indicated by a dashed arrow. (b) The wires of panel (a) mutually twisted, and (c) with proper extensions, as to create a dipole moment p, parallel to m. |
| In the text | |
 |
Figure 3. Simulated (left column) and measured (right column) magnitude of the transmission components (Txx: solid lines, Txy: dashed lines), for the fully metallic planar chiral metamaterials presented in Figure 1, and for linearly polarized incident wave [24]. The insets show the corresponding designs. |
| In the text | |
 |
Figure 4. Simulated transmission amplitudes |Txx| (upper panels) and |Txy| (lower panels), for the chiral metamaterials shown in Figure 1d, for linearly polarized incident wave [32]. One can see the cases of silver (black lines) and photoconductive silicon with σSi = 1 × 105 S/m (red lines) or 1 × 103 S/m (green lines) or 2.5 × 10−4 S/m (blue lines), respectively. The bottom panel shows the corresponding current distributions at the resonance frequencies for σSi = 1 × 103 S/m with Ey linearly polarized incident wave. |
| In the text | |
 |
Figure 5. Simulated optical activity, θ (solid lines), and ellipticity, η (dashed lines), for the switchable chiral structure under consideration [32]. One can see the cases of silver (black lines) and photoconductive silicon with σSi = 1 × 105 S/m (red lines) or 1 × 103 S/m (green lines) or 2.5 × 10−4 S/m (blue lines), respectively. The inset shows the corresponding design in which grey color corresponds to photoconductive silicon and yellow corresponds to metal (silver). |
| In the text | |
 |
Figure 6. (a) Schematic of the unit cell of the 3D SCR metamaterials under consideration [34]. The dimensions of the fabricated structure are ax = ay = 8.0 μm, az = 9.1 μm, w1 = 600 nm, and w2 = 850 nm, respectively. The wave propagation is along the z direction. (b) Top view of SEM image of the 3D SCR metamaterial, recorded at 15 kV. The magnification scale can be seen below the SEM image. |
| In the text | |
 |
Figure 7. (a) Simulated transmission components (absolute values) for linearly polarized incident waves propagating through the 3D SCR structure along the forward (positive) z-direction [34]. The red solid curve coincides with the blue solid curve. (b) Total transmitted amplitude for x- and y-polarized incident wave, |
| In the text | |
 |
Figure 8. Simulated optical activity, θ (blue solid line), and ellipticity, η, (red dashed line) for the wave transmitted through the 3D SCR metamaterials under consideration, when the metamaterial is excited by a x-polarized incident wave (Figure 6a) propagating along the forward z-direction [34]. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.