| Issue |
EPJ Applied Metamaterials
Volume 2, 2015
Advanced Metamaterials in Microwaves, Optics and Mechanics
|
|
|---|---|---|
| Article Number | 16 | |
| Number of page(s) | 9 | |
| DOI | https://doi.org/10.1051/epjam/2015010 | |
| Published online | 16 February 2016 | |
https://doi.org/10.1051/epjam/2015010
Research Article
RCS computations of targets with plasmonic coatings
CEA-CESTA, 33114
Bordeaux, France
* e-mail: Olivier.Vacus@cea.fr
Received:
29
July
2015
Accepted:
23
October
2015
Published online: 16 February 2016
As far as RADAR Cross Section (RCS) computations are concerned, metamaterial coating modeling issues lead to cases of millions of unknowns for targets greater than the wavelength. For computational limiting reasons, details of the coating cannot be meshed, even if they play a key role like in metamaterial design. Equivalent boundary conditions or effective medium approximation are then necessary. In this paper we consider spheres and cone-spheres with plasmonic coatings. Exact and approximated RCS computations are compared over a broad range of microwave frequencies. In the last section, we eventually point out the relevance of full-metallic grooved coatings in designing calibration objects exhibiting low RCS without the use of conventional RADAR Absorbing Materials.
Key words: Electromagnetic scattering / Radar cross-sections / Weston’s theorem / Electromagnetic modeling / Homogenization
© O. Vacus and C. Saint-Flour, Published by EDP Sciences, 2016
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Metamaterials (MTM) are often introduced as media exhibiting anomalous constitutive material parameters, such as non-positive electric permittivity (ε) and/or magnetic permeability (μ). It is perhaps more relevant to consider them first as complex structures at the microscopic scale, that is to say in the microwave domain, at a much smaller scale than the wavelength of interest λ. Typical MTM structures are indeed composed of more or less complex-shape inclusions such as spheres, wires, resonators or even holes (see [1] for a comprehensive introduction). As far as RADAR Cross Section (RCS) computations are concerned, meshing these inclusions to fit microscopic details would lead to unsolvable problems because target dimensions are much greater than λ. Consequently equivalent boundary conditions or equivalent material parameters are necessary, for instance for the design of a RAM coating which would be made up of stacks of alternating thin layers of a ferromagnetic metal and a dielectric material. Looking at Figure 1 in Section 2, one can easily imagine the architecture of such a coating; distances a and d would be of the order of a few micrometers. One would also have to take into account the finite electrical conductivity and the frequency-dependent magnetic permeability of the ferromagnetic material. For these reasons, a MTM approximation would be more suitable.
 |
Figure 1. Periodically grooved PEC sphere, with a the constant width of the grooves and d the spatial period. The grooves run along the φ direction so that the target has a rotational symmetry with respect to the z axis. |
Much work has been devoted to the computation of such material parameters (pioneer works are [2–4] or [6], while [7] can be seen as an interesting synthesis); they are known as “effective medium theories” or “effective medium approximations” (EMA) (see [8]). In most cases, modal expansions of the electromagnetic fields (E, H) are carried out under some periodicity assumptions and provide both equivalent dielectric permittivity and magnetic permeability μ. As for the existence of plasmons in metallic structures, a precursor analysis can be found in [9]. In this work we focus on the more recent results introduced by Garcia-Vidal et al. [11] in relation with perfect electrical conductors perforated with grooves; constitutive parameters are then characterized by functions of plasmon form, depending only on the geometry of the groove. More precisely, it is shown in [11], and further investigated in [12], that:
-
PEC boundary conditions in the grooves forces the electric field E to vanish and the dielectric permittivity can be deduced from extended Bruggeman theory [4];
-
the magnetic permeability must be modified to balance the effective index (here the product μ) so as to ensure a correct phase velocity in the grooves.
Our goal is to test these EMA results in RCS computations. This means that we do not consider electromagnetic fields in the vicinity of the perforated surface but only far field patterns (RCS is equal to the square modulus of these fields up to a constant). This must be seen as a global assessment, the object under test being considered as a whole. Moreover exact 3-D numerical tests are performed, rather than truncated analytical expansions: all the modes are here taken into account provided the discretization is fine enough. As we shall see, the EMA for plasmonic coatings derived in [12] is confirmed by our numerical approach based on far field comparisons.
Given any geometry, two different numerical models are required. The first one is expected to provide a reference solution to the scattering problem. This requires a precise meshing of the geometry of the coating of interest. The second one ignores the fine details of the coating and is used to test different EMA. Both models can run on a non-commercial code named SHFC based on a formalism involving a strong coupling of integral equations (method of moment) and finite volume elements to model PEC profiles and non PEC materials. The code currently deals with 2-D axi-symmetrical (see [5]) objects which explains the fact that the CPU time consumption remains low while producing accurate RCS even when the mean size of the elements tends to a fraction of wavelength.
As is often the case with RCS issues, spheres have been chosen as test object. Following the works described in [11] and [12], two kinds of grooved spheres are considered in this paper. Section 2 is devoted to a corrugated PEC sphere with parallel grooves of non constant depth, while Section 3 deals with radial grooves of constant depth. In both cases a short RCS analysis is proposed. Then results obtained from EMA are compared to exact RCS computations and discussed. A direct application to RCS calibration target design is detailed in Section 4. Conclusions are presented in Section 5. Preliminary results were reported in the conference papers [13, 20]. This article represents a comprehensive report of the final outcomes of our investigations.
2 RCS for plasmonic coating with parallel grooves
2.1 Geometrical description
In this section, we consider a textured PEC sphere as shown in Figure 1. The structure can be regarded as an inner PEC sphere of radius 96.5 mm coated with a periodically grooved PEC spherical shell having a uniform thickness of 3 mm. Periodicity along z is d = 5 mm. The grooves have a constant width a = 1 mm and a variable depth h which goes from a minimum value of 3 mm to a maximum mean value of 12.8 mm. Strictly speaking, since h is not constant, the overlaying structure would be better referred to as pseudo-periodic rather than periodic. The grooves are either empty or filled with a dielectric of permittivity εg. The target is assumed to rest in a standard air environment. In the following we shall be considering both TM-polarized (magnetic field H perpendicular to rz-plane, see Figure 1) and TE-polarized (electric field E perpendicular to rz-plane) incident plane waves propagating along the z-axis. RCS values are computed using the CEA home-made code SHFC briefly described in Section 1.
2.2 Exact RCS computation
All the results in this paragraph are obtained without any EMA. For this reason they are referred to below as exact RCS computations.
Figure 2 shows the zero incidence monostatic RCS of the textured PEC sphere compared to that of a plain PEC sphere having the same overall radius (99.5 mm), for frequencies over the range 100 MHz–42 GHz; the frequency step resolution is regular and equal to 1 MHz. For zero incidence, due to rotational symmetry, TM-RCS and TE-RCS are strictly identical. A frequency domain of high RCS with a maximum located at 30 GHz is readily noticed. This phenomenon is clearly identified as the onset of the 1st order scattering (νsc = c/2d = 30 GHz) at the Brillouin zone boundary. Extending the computations up to 100 GHz would have revealed the 2nd and the 3rd order diffractions at 60 and 90 GHz respectively. Such well-known diffractive effects are related to photonic band gaps and will not be discussed in this paper, where we focus on plasmonic behavior and low RCS.
 |
Figure 2. Exact RCS of the grooved sphere (red curve) compared to that of a plain PEC sphere (black dashed curve). |
The first low RCS region has a minimum at 5:8 GHz, which seems to correspond to the frequency location of a cavity waveguide mode inside the deepest groove:  ) with h = 12.8 mm and εg = 1 for empty grooves. This frequency would also be that of spoof surface plasmon polaritons on an equivalent flat PEC surface with regular 12.8 mm deep grooves [10–12]. Also, note that such an attenuation has been experimentally investigated in [15] in the case of a planar grooved metal structure.
) with h = 12.8 mm and εg = 1 for empty grooves. This frequency would also be that of spoof surface plasmon polaritons on an equivalent flat PEC surface with regular 12.8 mm deep grooves [10–12]. Also, note that such an attenuation has been experimentally investigated in [15] in the case of a planar grooved metal structure.
The second low RCS region extends from 21 to 25 GHz, with a minimum at 24.1 GHz, and seems to correspond to the frequency location of cavity waveguide modes inside a whole set of shallow grooves. Taking h = 3 mm, which is the depth of the central groove, leads to νsp = 25 GHz, while taking h = 3.5 mm, which is the mean depth of the 10th groove from the central position, leads to νsp = 21.5 GHz. If our assumptions are correct, we would expect νsp to be reduced by the factor  by merely filling the grooves with a dielectric of permittivity εg. This characteristic behavior is confirmed by the numerical results contained in Figure 3. Besides, as expected, it is clear on Figure 3 that the frequency location of the 1st order scattering (Brillouin zone) does not depend on the refractive index
by merely filling the grooves with a dielectric of permittivity εg. This characteristic behavior is confirmed by the numerical results contained in Figure 3. Besides, as expected, it is clear on Figure 3 that the frequency location of the 1st order scattering (Brillouin zone) does not depend on the refractive index  of the material filling the grooves.
of the material filling the grooves.
 |
Figure 3. Exact RCS of the grooved sphere showing the influence of the permittivity of the material filling the grooves. Red curve: εg = 1, blue curve: εg = 1.2, green curve: εg = 1.3. |
2.3 EMA in RCS computation
We now revert to the grooved PEC coating in Figure 1, looking for an adequate EMA.
A first approximation, denoted EMA0, is given by a straightforward homogenization, particularly with regard to μr and μφ. Using the extended Bruggeman theory (see [4] or [7]) leads to the set of characteristics: εz = 5, εr = εφ = –∞, μr = μφ = μz = 1. They define a first equivalent anisotropic coating which is modeled with finite volume elements in RCS computations. In practice, 1012 stands for 1 in our input data.
A second approximation, denoted EMAμ, follows the arguments developed in [11] for periodically textured PEC bodies or in [14] for lamellar composite materials. It reads: εz = 5, εr = εφ = –∞, μr = μφ = 0.2, μz = 1. These parameters define a new anisotropic coating. The distinctive feature of this model is related to the fact that diamagnetism has been introduced along the r and the φ directions. Thus the products εzμφ and εzμr remain equal to 1 ensuring that electromagnetic waves (Hr, Hφ, Ez) propagate along the empty grooves at the speed of light.
RCS results are contained in Figure 4. They show that the 3 mm grooved PEC coating is rather well-described by EMAμ (red curve), while EMA0 leads to an erroneous estimate of the RCS (blue curve): high RCS and low RCS zones are shifted down by a factor close to 2 due to an underestimated speed of propagation.
 |
Figure 4. Monostatic RCS at zero incidence. Green curve: exact computation for the periodically grooved PEC sphere. Blue curve: EMA0 or εz = 5, εr = εφ = –∞, μr = μφ = μz = 1. Red curve: EMAμ or εz = 5, εr = εφ = –∞, μr = μφ = 0.2, μz = 1. |
For off-axial incidences, TM-RCS and TE-RCS are no longer identical, which is in the nature of things. It is apparent from Figure 5 that the metamaterial approximation EMAμ at 2 GHz works very satisfactorily from the angular robustness standpoint. This low frequency has been chosen to ensure that the periodic step of 5 mm is small compared to the wavelength of 15 cm.
 |
Figure 5. Monostatic angular RCS at 2 GHz for TE (top) and TM (bottom) polarizations: green curve: exact computation; red curve: EMAμ computation; blue curve: EMA0 computation. |
The results are less convincing at higher frequencies, as shown in Figure 6 with TM-RCS and TE-RCS at 10 GHz. More precisely, a strong concordance is observed everywhere except for TM polarization around the direction normal to the main axis of the grooved sphere (z-axis). In this case the induced current J = H × n (where n is the outgoing normal unit vector) is normal to the grooves and the impact on the RCS is maximal. Every groove can be seen as a low bright point and the total RCS as the sum of a collection of different contributors since the depth of the grooves is varying along the current distribution. The observed differences can thus be explained by this non-constant depth and a slightly perturbed balance in the sum of contributions under the EMAμ assumption. Moreover, at 10 GHz, the periodic step of 5 mm is much closer to the wavelength which is now equal to 3 cm.
 |
Figure 6. Monostatic angular RCS at 10 GHz for TE (top) and TM (bottom) polarizations: green curve: exact computation; red curve: EMAμ computation; blue curve: EMA0 computation. |
To clarify those discrepancies, a second geometry of corrugation sphere is examined in the next section, with grooves of constant depth running along the surface.
3 RCS for plasmonic coating with radial grooves
3.1 Geometrical description
In this section, we consider a second textured PEC sphere as shown in Figure 7. With respect to the preceding grooved sphere, the structure has been modified in order to ensure a constant groove depth over the entire surface, via a radial distribution (a similar geometry is discussed in [12] for a PEC cylinder). Except for tapering effects, the elementary dimensions are comparable to those of the previous case: bottom width and depth are respectively equal to 1 and 3 mm, and the periodic step is equal to 5 mm.
 |
Figure 7. Second grooved PEC sphere. A rotational symmetry is conserved but the grooves are here radial. |
3.2 EMA in RCS computation
The same approximations as in the previous section are tested on this second grooved sphere, in the sense that the input permittivity and permeability tensors remain apparently unchanged: εθ = 5, εr = εφ = –∞, μr = μφ = μθ = 1 for EMA0 and εθ = 5, εr = εφ = –∞, μr = μφ = 0.2, μθ = 1 for EMAμ. However the new coordinates are now spherical in order to take into account the fact that the grooves are radial: the permittivity is equal to 5 along the direction perpendicular to the grooves (uθ), while the waves (Hr, Eθ) or (Eθ, Hφ) must still propagate along the grooves at the speed of light.
Monostatic RCS results at zero incidence is perfectly modeled by EMAμ over a broad range of frequencies (100 MHz to 15 GHz, see Figure 8), whereas EMA0 leads to erroneous results, even for low frequencies around 2 GHz.
 |
Figure 8. Monostatic RCS at zero incidence, from 100 MHz up to 15 GHz. |
This conclusion is confirmed by considering monostatic RCS as a function of incidence. As in the previous section, perfect concordance is observed at 2 GHz on Figure 9 between exact and EMAμ computations, while EMA0 turns out to be totally unsatisfactory. Moreover, the same comments hold here at 10 GHz (see Fig. 10), as opposed to the less convincing situation depicted in Figure 6, pertaining to the first PEC grooved sphere.
 |
Figure 9. Monostatic angular RCS at 2 GHz for TE (top) and TM (bottom) polarizations: green curve: exact computation; red curve: EMAμ computation; blue curve: EMA0 computation. |
 |
Figure 10. Monostatic angular RCS at 10 GHz for TE (top) and TM (bottom) polarizations: green curve: exact computation; red curve: EMAμ computation; blue curve: EMA0 computation. |
 |
Figure 11. Definition of a cone-sphere with a smooth tip. |
So, as suggested in the previous section, the differences observed in Figure 6 between exact and EMAμ computations are probably due to the varying depth of the grooves rather than to the small wavelength at 10 GHz. The successful test in the case of the constant depth radially distributed grooves seems to validate this assumption.
3.3 RCS analysis
Monostatic RCS results presented in Figure 8 are obtained with EMA0 and EMAμ approximations. For moderate frequencies (up to 2 GHz) they are rather similar, while for higher frequencies they exhibit a significant discrepancy. This calls for comment as both approximations lie roughly on the same kind of anisotropic tensors and a better agreement could have been expected. In particular, the very low levels of RCS obtained without any losses (e.g. less than −30 dBm2 around 11 GHz for EMA0) need an explanation.
This can be done using a standard surface impedance model. Let us consider a plane wave (k, E, H) defined in a spherical coordinate system (er, eθ, eφ): at null incidence k is parallel to er. The two terms of the anisotropic impedance tensor are denoted Z1 and Z2; they respectively satisfy the following relationships Eθ = Z1Hφ and Eφ = Z2Hθ.
Computing Z2 is straightforward. Due to the PEC conditions on the grooves, we have seen that εφ = –∞ which yields Eφ = 0 and Z2 = 0.
For impedance Z1 mode (k, Eθ, Hφ) must be considered. It is defined by finite value coefficients, respectively εθ = 5 and μφ = 1 for EMA0 and εθ = 5 and μφ = 0.2 for EMAμ. This leads for EMA0 to  , while for EMAμ we have
, while for EMAμ we have  . It turns out that Z1 tends to infinity when the tangent argument tends to
. It turns out that Z1 tends to infinity when the tangent argument tends to  . The thickness layer being 3 mm, this happens the first time (k = 0) respectively at f = 11.2 GHz for EMA0 and f = 25 GHz for EMAμ (see Sect. 4 for multiple frequency compensation). Assumptions of Weston’s theorem are then fulfilled (see [16] for the reference theorem and [17] for the anisotropic case):
. The thickness layer being 3 mm, this happens the first time (k = 0) respectively at f = 11.2 GHz for EMA0 and f = 25 GHz for EMAμ (see Sect. 4 for multiple frequency compensation). Assumptions of Weston’s theorem are then fulfilled (see [16] for the reference theorem and [17] for the anisotropic case):
-
the object is symmetrical,
-
impedance coefficients are reciprocal quantities:

This explains why the RCS vanishes. The first frequency can be readily checked on Figure 8 for EMA0. As for EMAμ, the RCS dip expected around 25 GHz can in fact be observed on extended computations of Figure 8 up to 30 GHz.
3.4 Non spherical objects
To check the validity of the EMA, we finally consider a cone-sphere, of main axis (0x) and defined by the three following parameters: α = 12.5 degrees the half-angle at the tip, r = 3 mm the small radius of the spherical part on the tip; R = 0.7 m, the large radius of the spherical part on the bottom. Junctions of the conical part and the two spherical parts are chosen to be tangent. The overall dimensions are approximately 4 × 1.4 × 1.4 m.
Anisotropic parameters are now introduced to describe a 3 mm layer surrounding the cone-sphere. They are defined in a local coordinate system (un, us, uφ): un is the unit outgoing normal vector; us is a unit tangential vector; uφ is a unit vector such that (un, us, uφ) is a direct orthonormal system. Thus the coordinate system can be chosen to be exactly the spherical coordinate system on the tip (small sphere) and the bottom (large sphere) of the cone-sphere. Following the computations performed in the spherical case, the electric permittivity is chosen to be a tensor equal to: while the magnetic permeability is chosen to be a tensor equal to:
while the magnetic permeability is chosen to be a tensor equal to:
RCS results are contained in Figure 12. The green curve (loose dots) refers to the exact RCS computation of a PEC cone-sphere derived from Figure 11, comprising an additional 3 mm PEC layer with periodic grooves of exactly the same nature as those represented on the sphere of Figure 7. The results demonstrate once again that EMAμ (red curve) is totally relevant on a broad band of frequencies. On the contrary EMA0 leads to a strongly inaccurate RCS (blue curve), with an error up to several tens of dB. These conclusions are confirmed by considering monostatic RCS as a function of incidence (see Fig. 13).
 |
Figure 12. Monostatic RCS at zero incidence. Green curve: exact computation for the periodically grooved PEC cone-sphere; blue curve: EMA0 computation; red curve: EMAμ computation. |
 |
Figure 13. Monostatic angular RCS at 6 GHz for TE (top) and TM (bottom) polarizations: green curve: exact computation; blue curve: EMA0 computation; red curve: EMAμ computation. |
4 Application to RCS calibration targets
A direct application of plasmonic coatings in the microwave domain is the design of calibration targets for RCS measurements. In anechoic chambers, the quality of RCS measurements is limited by couplings with the walls. New calibration targets are proposed to assess these couplings. The idea is to get null monostatic RADAR Cross Section at some desired frequency by designing suitable plasmonic coatings.
For the sake of simplicity, the following analysis is limited to spheres, but it is clear that more general 3-D shapes could as well be considered.
4.1 RCS calibration targets
RCS measurements simply amount to backscattering coefficient (Sd) measurements: 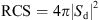 . In indoor anechoic chambers, as recalled above, it is first desirable to reduce reflections on walls or couplings by means of background subtraction, done by performing an empty room measurement. The next step is a standard calibration using a target with a precisely known RCS. Finally, in order to get accurate results, it turns out that 3 measurements are necessary: ST for the target under test, SC for the calibration target and S0 without any target (empty room):
. In indoor anechoic chambers, as recalled above, it is first desirable to reduce reflections on walls or couplings by means of background subtraction, done by performing an empty room measurement. The next step is a standard calibration using a target with a precisely known RCS. Finally, in order to get accurate results, it turns out that 3 measurements are necessary: ST for the target under test, SC for the calibration target and S0 without any target (empty room):
Here  denotes the theoretical RCS value of the calibration target, whose precise knowledge is obviously crucial. Any error on
denotes the theoretical RCS value of the calibration target, whose precise knowledge is obviously crucial. Any error on  yields the same error on the measurement. This explains why RAM are prohibited, for they give rise to unacceptable uncertainty. On the contrary, full-metallic targets are highly reliable; hence the interest of grooved plasmonic coatings as described in this paper: they offer a simple way to produce objects with RCS similar to those obtained with RAM, but without any specific constitutive parameters to control.
yields the same error on the measurement. This explains why RAM are prohibited, for they give rise to unacceptable uncertainty. On the contrary, full-metallic targets are highly reliable; hence the interest of grooved plasmonic coatings as described in this paper: they offer a simple way to produce objects with RCS similar to those obtained with RAM, but without any specific constitutive parameters to control.
4.2 A plasmonic X-band calibration sphere
Definition parameters as introduced in Section 2 have been optimized using EMAμ approximation in order to get null RCS in X-band and K-band. Sphere radius is now 298.5 mm, as indicated in Figure 14. Radial periodicity is d = 3 mm. The grooves have a constant width a = 0.6 mm and a constant depth 9 mm; the ratio a/d thus remains unchanged. Following indications of Section 3.3, expected frequencies such that Z1Z2 = 1 are given in Table 1.
 |
Figure 14. Definition of a calibration grooved sphere with null RCS in X-band and K-band. |
Comparison of predicted frequencies  and observed frequencies from exact RCS computations.
and observed frequencies from exact RCS computations.
A fine mesh is created to take into account the exact definition of the grooved sphere. Exact monostatic RCS computations are then performed with SHFC code from 100 MHz up to the Brillouin zone around 50 GHz. Results are depicted in Figure 15.
 |
Figure 15. Exact RCS of the grooved sphere as defined in Figure 14 (blue curve) compared to that of a regular sphere of same radius (green curve). Nearly null RCS frequencies are indicated by red dashed lines. |
As expected, three very low RCS are observed, up to 20 dB below the RCS level of a regular plain sphere of the same radius; they are indicated by vertical red dashed lines. Note that these frequencies are slightly different from those predicted using EMAμ approximation (see Table 1). It turns out that the electromagnetic waves do not propagate rigorously at the speed of light in our computations, but a little bit slower. Here it must be underlined that the relative shift is constant for the three frequencies. This would not have been the case if the shift had been caused by numerical dispersion. Indeed all the computations rely on the same meshing and the number of points per wavelength is five time greater at 8 GHz than at 40 GHz.
Taking this slight shift into account and in order to improve the accuracy of EMAμ approximation, a second-order correction might be brought to the diamagnetic permeability: μr = μφ = 0.21 might be preferred to ensure a better comparison between approximate and exact computations. This correction is not essential in our work, where exact computations remain possible as long as the target remains axi-symmetrical.
For frequencies immediately below the probing frequencies, that is to say around 6, 21 and 38 GHz, RCS is strongly oscillating, the mean value being equal to the RCS of the regular sphere. This can be properly established by using classical RADAR imaging techniques like range profiles. It is clear on Figure 16 that the specular contributor remains constant over the whole range. The only really low RCS levels are observed at the three expected frequencies (horizontal red dashed lines). At these frequencies, the monostatic RCS being negligible, standard measurements would allow to evaluate how strong is the coupling of the target with the anechoic chamber.
 |
Figure 16. Sliding range profiles computed between 1.6 GHz and 58.5 GHz (Δf = 3 GHz, δf = 100 MHz). Nearly null RCS frequencies are indicated by red dashed lines, as done in Figure 15. |
5 Conclusion
RCS computations represent an interesting approach to probe the behavior of plasmonic-like coatings in the MHz-GHz spectrum. They provide full-physics results, provided that the meshing is fine enough, averaged in the far field sense. For frequencies belonging to the range 100 MHz–12 GHz, the metamaterial effective medium approximation developed in [11] are definitely confirmed by our computations. They are thus entirely relevant as far as RCS is concerned and could be used with confidence for real 3-D issues (not necessarily axi-symmetrical objects). They have already been used in the design of new RCS calibration targets, plasmonic-like coatings being an interesting alternative to RAM. They have also provided reference results in computational RCS workshops [18, 19].
References
- N. Engheta, R.W. Ziolkowski, Metamaterials: physics and engineering explorations, Wiley, Germany, 2006. [Google Scholar]
- O. Wiener, Die Theorie des MischKorpers fur das Feld der stationaren Stromung, Ab Math. Sach Wiess 32 (1912) 506–604 [Google Scholar]
- K.W. Wagner, Erklarung der dielektrischen Nachwirkungsvorgänge auf Grund Maxwellscher Vorstellungen, Archiv. fur Elektretech. 2 (1914) 371–387. [CrossRef] [Google Scholar]
- D.A.G. Bruggeman, Berechnung verschiedener physikalischer Konstanten, Ann. Phys. 416 (1935) 636–664. [NASA ADS] [CrossRef] [Google Scholar]
- P. Bonnemason, B. Stupfel, Modeling high frequency scattering by axisymmetric perfectly or imperfectly conducting scatterers, Electromagnetics 13 (1993) 111–129. [CrossRef] [Google Scholar]
- J. Nevard, B. Keller, Reciprocical relations for effective conductivities of anisotropic media, J. Math. Phys. 26–11 (1985) 2761. [CrossRef] [Google Scholar]
- S. Berthier, Optique des milieux composites, Polytechnica (1993) . [Google Scholar]
- N. Mattiucci, R. Trimm, G. D’Aganno, N. Aközbek, M.J. Bloemer, Tunable narrow-band, all-metallic microwave absorber, Appl. Phys. Lett. 101 (2012) 141115. [CrossRef] [Google Scholar]
- J.B. Pendry, A.J. Holden, W.J. Stewart, I. Youngs, Extremely low frequency plasmons in metallic microstructures, Phys. Rev. Lett. 76 (1996) 4773–4776. [CrossRef] [PubMed] [Google Scholar]
- J.B. Pendry, L. Martin-Moreno, F.J. Garcia-Vidal, Mimicking surface plasmons with structured surfaces, Science 305 (2004) 847. [CrossRef] [PubMed] [Google Scholar]
- F.J. Garcia-Vidal, L. Martin-Moreno, J.B. Pendry, Surfaces with holes in them: new plasmonic metamaterials, J. Opt. A 7 (2005) S97–S101. [Google Scholar]
- A. Pors, E. Moreno, L. Martin-Moreno, J.B. Pendry, F.J. Garcia-Vidal, Localized spoof plasmons arise while texturing closed surfaces, Phys. Rev. Lett. 108 (2012) 223905. [CrossRef] [Google Scholar]
- F. Duverger, C. Saint-Flour, O. Vacus, RCS computations of targets with plasmonic coatings, Proc. Metamaterials 2013, Bordeaux, France, 2013. Poster Session 1.46 [Google Scholar]
- O. Acher, A. Adenot, F. Duverger, Fresnel coefficient at an interface with a lamellar composite material, Phys. Rev. B 62 (2000) 13748. [CrossRef] [Google Scholar]
- W. Liang, C. Jin-Xiang, L. You, L. Lei, D. Yin-Chang, W. Jian, Anomalous microwave reflection from a metal surface induced by spoof surface plasmon, Chin. Phys. B 21 (2012) 017301. [CrossRef] [Google Scholar]
- V.H. Weston, Theory of absorbers in scattering, IEEE Trans. AP 11 (1963) 578–584. [CrossRef] [Google Scholar]
- K.S. Yee, A.H. Chang, Scattering theorems with anisotropic surface boundary conditions for bodies of revolution, IEEE Trans. AP 39–7 (1989) 1041–1043. [Google Scholar]
- Q. Carayol, O. Vacus, Homogeneous anisotropic layer on a PEC cone-sphere, Proc. Workshop EM ISAE 2014, Toulouse, France, 2014. [Google Scholar]
- C. Saint-Flour, P. Soudais, O. Vacus, Modeling of plasmonic coatings in RCS computations, Proc. AP-S/URSI 2015, Vancouver, BC, Canada, 2015, Poster Session FRP-UC.1A.9. [Google Scholar]
- C. Saint-Flour, O. Vacus, Targets with plasmonic coatings for RCS calibration tests, Proc. 9th International Congress on Advanced Electromagnetic Materials in Microwaves and Optics – Metamaterials 2015, Oxford, England, 2015,Paper Oral Session. [Google Scholar]
Cite this article as: Vacus O & Saint-Flour C: RCS computations of targets with plasmonic coatings. EPJ Appl. Metamat. 2015, 2, 16.
All Tables
Comparison of predicted frequencies  and observed frequencies from exact RCS computations.
and observed frequencies from exact RCS computations.
All Figures
 |
Figure 1. Periodically grooved PEC sphere, with a the constant width of the grooves and d the spatial period. The grooves run along the φ direction so that the target has a rotational symmetry with respect to the z axis. |
| In the text | |
 |
Figure 2. Exact RCS of the grooved sphere (red curve) compared to that of a plain PEC sphere (black dashed curve). |
| In the text | |
 |
Figure 3. Exact RCS of the grooved sphere showing the influence of the permittivity of the material filling the grooves. Red curve: εg = 1, blue curve: εg = 1.2, green curve: εg = 1.3. |
| In the text | |
 |
Figure 4. Monostatic RCS at zero incidence. Green curve: exact computation for the periodically grooved PEC sphere. Blue curve: EMA0 or εz = 5, εr = εφ = –∞, μr = μφ = μz = 1. Red curve: EMAμ or εz = 5, εr = εφ = –∞, μr = μφ = 0.2, μz = 1. |
| In the text | |
 |
Figure 5. Monostatic angular RCS at 2 GHz for TE (top) and TM (bottom) polarizations: green curve: exact computation; red curve: EMAμ computation; blue curve: EMA0 computation. |
| In the text | |
 |
Figure 6. Monostatic angular RCS at 10 GHz for TE (top) and TM (bottom) polarizations: green curve: exact computation; red curve: EMAμ computation; blue curve: EMA0 computation. |
| In the text | |
 |
Figure 7. Second grooved PEC sphere. A rotational symmetry is conserved but the grooves are here radial. |
| In the text | |
 |
Figure 8. Monostatic RCS at zero incidence, from 100 MHz up to 15 GHz. |
| In the text | |
 |
Figure 9. Monostatic angular RCS at 2 GHz for TE (top) and TM (bottom) polarizations: green curve: exact computation; red curve: EMAμ computation; blue curve: EMA0 computation. |
| In the text | |
 |
Figure 10. Monostatic angular RCS at 10 GHz for TE (top) and TM (bottom) polarizations: green curve: exact computation; red curve: EMAμ computation; blue curve: EMA0 computation. |
| In the text | |
 |
Figure 11. Definition of a cone-sphere with a smooth tip. |
| In the text | |
 |
Figure 12. Monostatic RCS at zero incidence. Green curve: exact computation for the periodically grooved PEC cone-sphere; blue curve: EMA0 computation; red curve: EMAμ computation. |
| In the text | |
 |
Figure 13. Monostatic angular RCS at 6 GHz for TE (top) and TM (bottom) polarizations: green curve: exact computation; blue curve: EMA0 computation; red curve: EMAμ computation. |
| In the text | |
 |
Figure 14. Definition of a calibration grooved sphere with null RCS in X-band and K-band. |
| In the text | |
 |
Figure 15. Exact RCS of the grooved sphere as defined in Figure 14 (blue curve) compared to that of a regular sphere of same radius (green curve). Nearly null RCS frequencies are indicated by red dashed lines. |
| In the text | |
 |
Figure 16. Sliding range profiles computed between 1.6 GHz and 58.5 GHz (Δf = 3 GHz, δf = 100 MHz). Nearly null RCS frequencies are indicated by red dashed lines, as done in Figure 15. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


