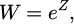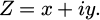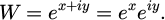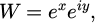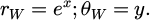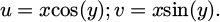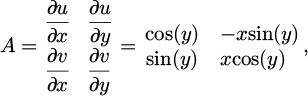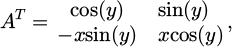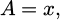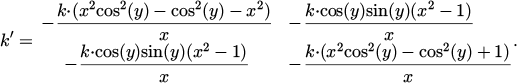| Issue |
EPJ Appl. Metamat.
Volume 9, 2022
|
|
|---|---|---|
| Article Number | 19 | |
| Number of page(s) | 5 | |
| DOI | https://doi.org/10.1051/epjam/2022017 | |
| Published online | 13 December 2022 | |
https://doi.org/10.1051/epjam/2022017
Research Article
Metamaterials simulation for thermal diffusers
Centro de Investigación en Materiales Avanzados, S.C., Materials Physics Department, Miguel de Cervantes 120, Chihuahua 31136, Chih., Mexico
* e-mail: luis.alfonso.nb1111@gmail.com
Received:
16
July
2022
Accepted:
10
November
2022
Published online: 13 December 2022
The heat extraction efficiency of a cylindrical diffuser can be optimized by applying differential geometry [J.-P. Huang, Theoretical Thermotics: Transformation Thermotics and Extended Theories for Thermal Metamaterials (Springer, 2020)], in order to find a metamaterial design. That can be done by coupling a thermally insulating material (polytetrafluoroethylene) with a high thermal conductivity material (copper) where the heat flow is directed. By controlling the distance between the isothermal contours, to extract the heat while maintaining a constant temperature gradient along the diffuser avoiding heat accumulation.
Key words: Metamaterial / polytetrafluoroethylene (PTFE) / copper / isothermal contour / diffuser
© L.A. Nuñez-Betancourt and J.A. Matutes-Aquino, Published by EDP Sciences, 2022
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Metamaterials represent an exciting emerging research area that promises to bring important technological and scientific advances in various areas such as telecommunications, radar and defense, nanolithography with light, microelectronics, medical imaging, etc. There is currently no universal definition of metamaterials; generally speaking, metamaterials are artificial media with unusual properties [1].
Initially metamaterials were mainly used in the field of electromagnetism [2–5]. Their general goal was to create invisibility cloaks for low-frequency waves such as microwaves [3,4], the idea was based on a phenomenon called transformation optics, achieves the deformation of the path that the wave travels avoiding the collision with objects on their way.
Sometime later it was shown that the phenomena of transformation optics could be applied to other branches of physics, such as heat transfer [6]. This proposed new phenomena such as thermal invisibility cloaks, thermal rotors, heat concentrators, and thermal diffusers.
Thermal metamaterials fulfill a specific function by designing in the manipulation of the heat flow and the distribution of its thermal energy with the transformation of coordinates. Depending on the desired application, they can have continuous heat flow lines, which can be directed at specific points, thanks to the lack of coincidence in thermal conductivities in local areas. With this feature, it can be deduced that thermal metamaterials contain a property for the control of heat flux lines in local areas. These lines of heat flux can be manipulated by changing the thermal conductivity in the direction where the heat flux is flowing, facilitating flow in the desired direction and avoiding flow at inconvenient points [7].
Figure 1 shows the control of the heat flow by using a copper plate with PTFE-filled cuts inclined 45° with respect to the horizontal. Because there is an abrupt change in the thermal conductivity in the material, the heat tends to change its propagation direction following the direction of the higher thermal conductivity and not the higher temperature gradient, as should be expected according to Fourier's law for heat conduction, which indicates that the heat flux goes in the direction of the gradient of temperature.
It is common, that in certain thermal applications, rapid dissipation of thermal energy from a heat source is desired, and that, in turn, it follows a precise route for heat transfer. Therefore, an efficient heat transfer is constantly sought. It was thought that the optimal thermal dissipation could be given by homogeneous and isotropic materials with spherical symmetries for point heat sources or cylindrical symmetries for linear heat sources.
However, it has been shown that the isotropic thermal conductivity for these symmetries is inefficient because it produces a nonlinear temperature gradient (see Fig. 3), and generates unwanted hot spots. A linear temperature gradient can be obtained using an anisotropic design to eliminate these deficiencies [8].
A cylindrical or spherical symmetry can present a good challenge at the time of its design, but these symmetries also present a wide field of applications in the design of thermal metamaterials [9], in this case the design of a thermal diffuser with cylindrical symmetry is sought to find a new way to dissipate heat more efficiently.
Currently, the manufacture of metamaterials presents a more complicated case than their design, and for this reason, new and more complex ways of designing metamaterials are constantly considered. In turn, their manufacture is facilitated, leaving aside anisotropic materials while looking for the coupling of different isotropic materials, which when combined, present new thermal properties [10].
In this study, the coupling between a thermal insulating material, polytetrafluoroethylene (PTFE) and a thermal conductor material (Cu) was sought, in order to find, through a geometric arrangement, the control of the heat flow, so it behave as an ideal thermal diffuser [8].
 |
Fig. 1 Thermal signature (°C) in the simulated unit cell to direct heat at a 45° tilt (left), heat flux in the unit cell (right). |
2 Design
2.1 Geometry transformation
To find an optimal design for the metamaterial, it is necessary to propose a model in which the heat transfer is as fast as possible. Through functions of complex variables and conformal mapping [11], W = e Z establishes a relationship between a real space W and a virtual space Z for the transformation of a rectangle (which has a linear temperature gradient) into a half disk (which has a non-linear temperature gradient). This relationship maintains the geometric object and its thermal characteristics (in this case, a linear temperature gradient) in different geometries.
Thus,
If we consider polar coordinates
Therefore, it is obtained that
And through this relationship, it is obtained that an object can be considered with a different geometry for different spaces, but it is still the same geometric object (see Fig. 2).
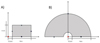 |
Fig. 2 Conformal mapping in virtual space (A) and its transformation into real space (B). |
2.2 Transformation for thermal conductivity
Using the heat equation under the coordinate transformation for a change of space [12], we have the matrix equation for the transformation of the thermal conductivity from virtual space to real space, maintaining the thermal characteristics in both spaces.
In this case, a two-dimensional matrix was used to analyze the disk, where A is the Jacobian matrix of partial derivatives for the coordinate transformation, A T is the transpose matrix of the Jacobian matrix, and detA is the determinant of said matrix.
With this transformation of the thermal conductivity, it is possible to obtain the same linear temperature gradient in a different geometry, since it is the same geometric object [13].
2.3 Simulation and application
With the data obtained, a simulation of a steady state study is carried out to analyze the behavior of both materials. Temperature in the internal radius of the disk, T i = 120 ° C, and the temperature at the outer radius of the disk, T o = 20 ° C.
As can be seen in Figure 3 for the theoretical metamaterial with anisotropic thermal conductivity there is a linear temperature gradient (as would occur in the case of rectangular geometry), even though it is a geometry that does not have these characteristics. On the other hand, the isotropic material has a temperature gradient whit a slope that varies at each point (an inefficient way since it genere hot spots and limits the constant heat flux).
However, finding a geometric configuration that follows the heat flow directions found in an anisotropic material can be a very complex problem. Therefore, the approach in metamaterial design for this work is based on the design of isothermal contours for the metamaterial.
For an isotropic material, the isothermal contours present a separation between them that increases as it moves away from the center of the disk (Fig. 4A). As it has been shown in Figure 3, it considers constant temperature changes, which can be translated as a non-linear temperature gradient. Meanwhile, in the anisotropic metamaterial, equidistant isothermal contours are presented (Fig. 4B) for constant temperature changes, which can be understood as a linear temperature gradient.
 |
Fig. 3 Temperature gradient for the theoretical ideal anisotropic diffuser (black) and a conventional isotropic copper diffuser (red). |
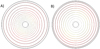 |
Fig. 4 Isothermal contours of an isotropic copper material (A) and an anisotropic material (B). |
2.4 Design of the metamaterial through isothermal contours
Taking into account that the isothermal contours can be considered for the design of the metamaterial, a simulation of a study in steady state is carried out for a copper plate with cuts filled with PTFE, forming concentric semicircles. It can be seen in Figure 5 to that isothermal contours are established in the area where the material with low thermal conductivity is located.
With these considerations, a design for the metamaterial is established, making concentric and equidistant cuts on the copper disc with a separation of 1.1 mm between each cut and 1 mm width of the cut. The cuts are filled with PTFE. In addition, an azimuthally distributed spacing in 16 segments of 2 mm width is proposed, in order to allow heat flow to the outer contour of the disk.
In this way, it is expected that the isothermal contours are established in the area of the cuts. Since the cuts are equidistant, the isothermal contours should be too.
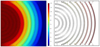 |
Fig. 5 Temperature signature for a unit cell with concentric circular cuts (left), Isothermal contours established in the area of the unit cell cuts (right). |
3 Results and discussion
When performing a simulation of a study in steady state for the proposed design, the conditions that are shown in Figure 3, shows us that the isothermal contours are equidistant, see Figure 7, and established by the cuts made in the disc, see Figure 6. In this way a temperature gradient is obtained that approximates the linear temperature gradient of the anisotropic metamaterial. To analyze the variation of the data, several measurements were made at different points for the temperature gradient. Once it was shown that all were the same (the gradient does not change when the measurement point varies), they were compared against the isotropic and anisotropic materials (Fig. 8) showing that the data obtained are quite close to the desired ones.
The isothermal contours were established in the area of the PTFE-filled sections due to the abrupt change in thermal conductivity. This condition allowed equidistant isothermal contours to be established.
As shown by conformal mapping and coordinate transformation, it was possible to arrive at a model in which the temperature gradient was close to that of an ideal diffuser. The model presented no hot spots or strong temperature changes are while maintaining equidistant isothermal contours and a heat flux that allowed constant cooling.
These designed properties can be modified and adapted to different needs. It depends on the thermal properties of the materials used, the thickness and distance of the cuts, a smaller number of cuts and a higher thermal conductivity of the insulating material. These properties allowed for greater heat transfer because they allow thermal energy to be expelled more quickly. However, these changes compromise the behavior of the proposed metamaterial, affecting the linearity of the temperature gradient. The measures used were established to allow the gradient of temperature to remain linear allowing the maximum possible heat flow.
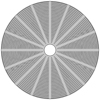 |
Fig. 6 Proposed design for metamaterial using PTFE-filled cuts in a copper cylinder. |
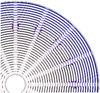 |
Fig. 7 Isothermal contours for the proposed metamaterial. |
 |
Fig. 8 Temperature gradient for an anisotropic metamaterial (black), isotropic copper (red) and the proposed metamaterial (blue). |
4 Conclusions
A theoretical anisotropic thermal metamaterial for a heat diffuser was designed using complex variable conformal mapping.
Compared to a heat spreader made from isotropic copper, the metamaterial heat spreader has a linear temperature gradient which removes heat faster and prevents hot spots.
For practical considerations, the theoretically designed anisotropic thermal metamaterial was made with a combination of two suitable sets of isotropic materials: PTFE with low thermal conductivity and copper with high thermal conductivity. This characteristic is what allows the heat flow to be directed specifically. Applying Fourier's law of heat conduction, it was shown that an abrupt change in thermal conductivity can give more priority to the direction of heat flow in the direction of high thermal conductivity instead of the largest temperature gradient.
The practical metamaterial temperature gradient is a very good representation of the theoretically designed anisotropic thermal metamaterial temperature gradient.
References
- G.V. Eleftheriades, K.G. Balmain, Negative-Refraction Metamaterials − Fundamental Principles and Applications (Wiley, 2005) [CrossRef] [Google Scholar]
- V.G. Veselago, The electrodynamics of substances with simultaneously negative values of ɛ and µ, Sov. Phys. Uspekhi 10, 509 (1968) [CrossRef] [Google Scholar]
- D.R. Smith, W.J. Padilla, D.C. Vier, S.C. Nemat-Nasser, S. Schultz, Composite medium with simultaneously negative permeability and permittivity, Phys. Rev. Lett. 84, 4184 (2000) [CrossRef] [Google Scholar]
- J.B. Pendry, A.J. Holden, D.J. Robbins, W.J. Stewart, Magnetism from conductors and enhanced nonlinear phenomena, IEEE Trans. Microwave Theory Tech. 47, 2075 (1999) [Google Scholar]
- J.B. Pendry, A.J. Holden, W.J. Stewart, I. Youngs, Extremely low frequency plasmons in metallic mesostructures, Phys. Rev. Lett. 76, 4773 (1996) [CrossRef] [Google Scholar]
- C.Z. Fan, Y. Gao, J.P. Huang, Shaped graded materials with an apparent negative thermal conductivity, Appl. Phys. Lett. 92, 251907 (2008) [CrossRef] [Google Scholar]
- G. Park, S. Kang, H. Lee, W. Choi, Tunable multifunctional thermal metamaterials: manipulation of local heat flux via assembly of unit-cell thermal shifters, Sci. Rep. 7, 41000 (2017) [CrossRef] [Google Scholar]
- K.P. Vemuri, P.R. Bandaru, An approach towards a perfect thermal diffuser. Sci. Rep. 6, 29649 (2016) [CrossRef] [Google Scholar]
- S. Yang, J. Wang, G. Dai, F. Yang, J. Huang, Controlling macroscopic heat transfer with thermal metamaterials: theory, experiment and application, Phys. Rep. 908, 1 (2020) [Google Scholar]
- K.P. Vemuri, P.R. Bandaru, Geometrical considerations in the control and manipulation of conductive heat flux in multilayered thermal metamaterials, Appl. Phys. Lett. 103, 133111 (2013) [CrossRef] [Google Scholar]
- R.V. Churchill, J.W. Brown, Complex Variables and Applications, 8th edn. (McGraw-Hill Science, 2008) [Google Scholar]
- T. Han, C.-W. Qiu, Transformation Laplacian metamaterials: recent advances in manipulating thermal and dc fields, J. Optics 18, 044003 (2016) [CrossRef] [Google Scholar]
- J.-P. Huang, Theoretical Thermotics: Transformation Thermotics and Extended Theories for Thermal Metamaterials (Springer, 2020) [CrossRef] [Google Scholar]
Cite this article as: Luis Alfonso Nuñez-Betancourt, José Andrés Matutes-Aquino, Metamaterials simulation for thermal diffusers, EPJ Appl. Metamat. 9, 19 (2022)
All Figures
 |
Fig. 1 Thermal signature (°C) in the simulated unit cell to direct heat at a 45° tilt (left), heat flux in the unit cell (right). |
| In the text | |
 |
Fig. 2 Conformal mapping in virtual space (A) and its transformation into real space (B). |
| In the text | |
 |
Fig. 3 Temperature gradient for the theoretical ideal anisotropic diffuser (black) and a conventional isotropic copper diffuser (red). |
| In the text | |
 |
Fig. 4 Isothermal contours of an isotropic copper material (A) and an anisotropic material (B). |
| In the text | |
 |
Fig. 5 Temperature signature for a unit cell with concentric circular cuts (left), Isothermal contours established in the area of the unit cell cuts (right). |
| In the text | |
 |
Fig. 6 Proposed design for metamaterial using PTFE-filled cuts in a copper cylinder. |
| In the text | |
 |
Fig. 7 Isothermal contours for the proposed metamaterial. |
| In the text | |
 |
Fig. 8 Temperature gradient for an anisotropic metamaterial (black), isotropic copper (red) and the proposed metamaterial (blue). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.